Week 1 - Introduction to ArcGIS and acquiring new data

Classroom topics:

• Structure of the class.

• Introduction to GIS
• Applications in anthropology
• Strengths, weaknesses, and critiques
• Topics we will cover in this 10 week course

In Class Lab -- Week 1

Part I - Create a shapefile and digitize from a satellite image.

In this exercise we will learn how to create a polygon shapefile by digitizing the polygon from an satellite image of the pyramids of Giza.

1. We will begin by downloading files from the class download directory. Download Giza_image.zip and pyramids.zip.
2. Go to ArcCatalog and create a folder called "Giza". In that folder, create a polygon shapefile with one Text string attribute field called 'Title'.
3. Unzip and add the "Giza_image" jpeg to an Arcmap project.
4. Digitize two of the pyramids as polygons by starting an edit session. Once you have drawn them, open the attribute table and name these pyramids "Pyramid 1" and "2" in the Title Field. Change the symbology to hollow red shapes and label the shapes using the Title field.
5. You've just done "heads up digitizing" on a satellite image.

 

Part II - How to import point locations from an XY table.

1. In Part I you downloaded a CSV file called Pyramids.csv. These are data I got from a GoogleEarth blog site showing the locations of many pyramids in Egypt and a few in the Americas. Double-click the table file in Windows so you can view it in Excel. Note that the first line, which become field headings, consist of simple and short words. The table was Comma-delimited format (.CSV = comma-separated variables).
2. Import the CSV file into Arcmap using the "Add XY..." command. As you saw, there is the Name column, and then coordinates in Latitude and Longitude and decimal degrees. Which column of values do you think goes in the X column and which goes in Y? Make sure that the data is assigned to the Geographic "WGS1984" coordinate system.
3. The file is imported as an "event theme". You should see the points fall right where the pyramids that we digitized are located. If the new points don't fall within the polygons you digitized then there's a problem... maybe you needed to import Longitude as the X value and Latitude as the Y value?
4. We want to convert these data to a regular point Shapefile. Make sure no features are selected, and then right click the layer and choose "Export Data..." to convert these data to shapefile. Remove the original Events layer from the Table of Contents. Load the new data into your view (and remove the Events theme). Label these points by right-clicking the new Shapefile data layer in Arcmap and choosing "Label features".

You just brought in raw point data from an XY text table. This is a very powerful technique for importing raw data tables from books, data sets online, and a variety of input tools like GPS units, total stations, laser transits.

Part III - In which countries are these pyramids found?

1. To answer this question we need to download some reference datasets. Go to this data folder http://www.mapaspects.org/gis/data/ and go to /vectors/world/ and download "Admin_boundaries2004.zip" to your work space. These are data showing National and State (Provincial) level regions in a WGS1984, Decimal Degree reference system.
2. Unzip and this folder and add these data to your view. Drag the Admin layer to the bottom of the Table of Contents so that these large polygons don't obscure the other layers.
3. By using a spatial join we can have the attributes of the Admin layer appended to the Pyramids layer. Right click "Pyramids" shapefile point layer and go to Join... and then at the top of the Join box choose the box to Join using spatial location. Join to the Admin layer and call the output file "Pyramids_Admin".
4. Open the attribute table of the resulting file. Note that the 38 rows of pyramid data now have Admin table data appended to the right. Scroll right to see these data. Sort the table by Country by right-clicking the CNTRY_NAME field and choosing Sort Ascending.
5. How many pyramids are in each Administrative area? This question is answered easily by right-clicking the ADMIN_NAME field title and choosing "Summarize...". At the bottom of the dialog name the file "Admin_Pyramids_Table". The output appears in your table of contents. There should be four rows (admin areas with pyramids) and the COUNT of pyramids in each zone. Here we found that using generic administrative data can be useful in a number of ways.

• you can use it to visually confirm that your data lines up with other "objective" data from other sources.
• you can use it to compare your own datasets with familiar administrative categories for reports and other summary functions.

As you can see a powerful part of GIS is the ability to combine tabular data with geographical location. The Spatial Join function is very useful for combining datasets that are not otherwise compatible because they use different indexing systems or naming conventions, or they are in different languages. The common reference of spatial position brings them together.

Week 2 - Data organization and management

Exercises:

• Restructuring a 1:M table
• Proportion of obsidian artifacts

Classroom Topics

This week's class will focus on data organization and management for GIS applications to anthropological research. Specifically, we will spend time discussing the importance of relational databases and means of organizing and querying data organized into related tables.

I will also describe approaches to indexing data for anthropological fieldwork. The ID number system at various spatial scales and methods for linking tables between ID number series.

 

In Class Lab Exercises, week 2

In lab this week we will focus on a-spatial data management techniques in ArcGIS. Joining and relating tables is are powerful tools, but it also creates a structure that can make queries and representation more difficult.

 

Download Callalli Geodatabase.

Look the data in Arcmap.

• There are a few major file groups: Ceramics, Lithics, Sites
• What is the function of these fields: ArchID, CatID, LocusID, SiteID

Display. Turn off ArchID_centroids.

• show sites as tan, ceramics as red, lithics as lt green. Orange circles = sherds, green triangles = points.
• hydrology = blue. Lg river, small river.

Discuss file formats: coverages, shapefiles, GDB. Raster / GRID.

 

Problem 1:

Ceramics Lab results. Cleaning up the database logic.

Working at the artifact level of analysis the ID number system is problematic because you cannot refer to a single artifact from an index field.

What are some solutions?

1. Open the Ceramics_Lab2 attribute table.

• Click Add field… in the menu below.
• Create a Long Integer field and call it “ArchCat”. Make a second one called “ArchCat_temp”
• Do you see both ArchCat fields in the table? Scroll to the right.
• Make sure no rows are selected before the next step
• Right click the “ArchCat_temp” field title column
• Choose “Calculate Values…” in the menu.
• Multiply the contents of ArchID by 1000 into this field.
• Right click the “ArchCat” field title column
• Choose “Calculate Values…” in the menu.
• Add the contents of “CatID” to “ArchCat_temp” into this field.

Do you now have a six digit ID#? That’s your new unique ID number that allows you to refer to individual artifacts.

2. Cut off the “diameter” measure for more efficient design

This is somewhat extreme "database normalization", but you can see the principal behind it.

• Right click the Diameter column and sort Descending.
• Select in blue the rows with values > 0
• Click Export… and save to a new table called Rim_Diameters
• Look at the new table. Where is your ArchCat field? It’s back on the right side. The goal here is to have a very efficient database structure with little redundancy and minimal empty cells.
• Open the toolbox (red toolbox in the top toolbar) and go to Data Management Tools > Fields > Delete Fields…
• Choose the RimDiameters table.
• Select All, then uncheck “Diameters” and “ArchCat” (at the end of the list).
• Go to the Ceramics_Lab2 table and delete the Diameters field.
• Right click the Ceramics_Lab2 table and click “Joins and Relates… > Join” and join the table to Ceramics table to the RimDiameters table. Think about the fields that you will use to join. Is this a One-One or a One-Many link?

Other selection methods. Try selecting data in the Ceram_p (not the lab file) file using Select by Attributes. The text you enter in the box is a modified SQL query. Try to select all of the Bowls from the LIP period and look at the selection on the map.

 

Problem 2:

Show relationship between size the archaeological site (m2) and proportion of obsidian artifacts in the lab2 analysis.

The basic problem here is that there are MANY fields in each site. In order to represent the data on the many site we need to collapse the contents of the Many table into units so the One table can symbolize it.

Steps:

1. Problem. You’ve explored the data in Site_A and in Lithics_Lab1 and you recognize that you have to collapse the values in Lithics_Lab1 before you can show them on the map. You can collapse table values with a tool called Pivot Tables and then by Summarizing on the SiteID column.

First, make sure there are no row selected in the "Lithics_Lab1" table.

Open the Pivot Tables function in the toolbox under Data Management > Tables > Pivot Tables

2. Pivoting the data table. In the Pivot Tables box select “Lithics_Lab1” as your pivot table. This is the table that has the quantity of data we want to reduce. We are effectively swapping the rows and columns in the original table.

• Click in the Input fields box and read the Help on the right (click Show Help button if it’s not on).
• “Define records to be included in the pivot table”. Think about this… we can only link these lab results to space if we can tie them to spatial units. Space, in this exercise, is defined by SITE areas. Therefore we ONLY want to deal with data in terms of the site that falls into. If you have records logged by other criteria other (too many boxes checked) you would have too many rows in your pivot table and it will not mesh with the Site_A feature. Therefore select only SITEID.
• Click in the Pivot Field box and read the help. “Generate names of the new fields”. Fields are columns in tables therefore you are choosing the field that will become your column headings. We are trying to distinguish Obsidian from non-obsidian therefore pick MATERIAL.
• Click in the Value field and read the help. “Populate the new fields”. In other words this is the value be summed for each site per material type. Chose Peso_Orig (spanish for Weight, measured in grams).
• The result should include the following: for each site with obsidian or non-obsidian we will add report the weight of each material in separate columns that can easily be summed.

You can use the default filename. It should end up in your geodatabase. Have a look at the contents of the output table. Note that there many SITEID values that are NULL. That is because there were artifacts collected outside of sites in some cases. Note, also that the MATERIAL TYPE values have become column headings (Obs, NotObs), but there are still duplicate sites in rows as you can see in the SITEID column.

• We need to Summarize by the SITEID column in order to collapse these into a single line per Site. right-click the title and go to Summarize on SITEID.
  
• Next, check sum in "Obsidian" and check sum in "Not Obsidian". Name the table "Obsidian_by_Site".

Look at the resulting table. Is there only one SITEID value per row? Why are there so many with a <NULL> SITEID value? Where did that data come from?

3. Representing the data. Now that the results for each site is found on a single line you can Join it to the Site_A feature.

• Right-Click the Sites_A feature and go down to Joins and Relates… and choose Join…
• Make sure the top field is for “Attributes from a Table”. Then jump down to the #2 question in the middle and choose your output Pivot Table from Step 2. Next, select the appropriate fields in fields #1 and #3 on which to base a join. You should be able to join ARCHID in the Site table with SITEID in the pivot table.
• Click “Advanced…” and read the different descriptions. This distinction is also known as the “Outer Join” vs “Inner Join” relationship. Choose “matching records” (i.e., inner join, or exclusive rather than inclusive join).

Look at the resulting table. Does it contain all the information you need collapsed onto rows? Look at the number of records. There were 88 in the original Site_A table, now there are fewer (or there will be if you update by scrolling down the table). Why is that? The original question asked about the relationship between site size and presence of obsidian. How are you going to measure site size?

4. Symbolizing the data. You can show these data using a number of tools. For example, for a simple map you could divide the weight of obsidian by the weight of non-obsidian per site and symbolize by the ratio of obsidian over non-obsidian.

Here, we will do something slightly more complex and use a pie chart to show the relationship with respect to size.

• Go to Sites > Properties > Symbology…
• Choose Show > Charts… > Pie
• Choose the bottom two fields on the Field Selection and click the right arrow.
• Change the colors of the two fields you selected to two contrasting fields.
• Click OK and look at the result.
• What about the size of the site? Click Site_A Properties > Symbolize … again
• Click the Size… button at the bottom center. Choose “Vary size using a Field…” and choose “Shape_Area” as the Size.. field and “Log” as the Normalize field.

Zoom in and out and notice how the symbols change as you pan around. Zoom way in. It looks better that way, doesn't it?

Experiment with other ways of symbolizing these data.

Save this project, we will work on it more later.

Homework

As mentioned in class, next week we will focus on methods of bringing data into GIS. Which project area do you plan to work in? We will begin constructing acquiring data (imagery and topographic data) next week so please decide on a project area by then.

You will need Latitude/Longitude coordinates in WGS1984 for the four corners of a bounding box around your study area. An easy way to get these values in in GoogleEarth. You'll want to pick a region about the size of a County in the US for this assignment.

Write down these four corner coordinate values. We'll use them in class next week.

 

Week 3 - Acquisition of digital data

Exercises: finding datasets, global coverage:

• Georeferencing scanned historic maps
• Importing GoogleEarth imagery to Arcmap
  
• Locating topographic data
• Locating multispectral imagery
• Locating vector data

Classroom Topic:

Data acquisition methods for anthropological research.

Exercises: finding datasets, global coverage:

• Georeferencing scanned historic maps
• Importing GoogleEarth imagery to Arcmap
  
• Locating topographic data
• Locating multispectral imagery
• Locating vector data

Classroom Topic:

Data acquisition methods for anthropological research.

This class session will focus on means of incorporating new and existing datasets into a GIS environment.

• GPS and mobile GIS methods.
• Remote sensing overview: local (GPR, magnetometry) and airplane/satellite-based sensors.
• Total station: high resolution, large scale data
• Importing and restructuring existing data sets, spatial and aspatial.

Incorporating new and existing data into a GIS is a major obstacle to applying digital analysis methods to anthropological research. How do you acquire digital data in remote locations with poor access to electricity? How do you reconcile the differences in scale between

1. fine resolution: excavation data, millimeter precision, total station
2. medium resolution: surface survey data and GPR/mag data, ~1m accuracy, GPS
3. coarse resolution: regional datasets, 10-90m accuracy, imagery and topography
4. existing data: tabular and map data at various scales from past projects.

These methods deserve a one quarter class apiece and there is insufficient time to go into detail on remote sensing or total station data acquisition.

In Class Lab Exercises, Week 3:

PART I. Georeferencing existing map data

This week we will focus on the input of digital data. There are a variety of imagery and scanned map sources available on the web and in the first exercise you will georeference a scanned map of South America (7mb).

Note that this JPG map has Lat/Long coordinates on the margins of the map. These will allow us georeference the data provided we know the coordinate system and datum that the Lat/Long gradicule references. If we did not have the Lat/long gradicule we may be able to do without it by georeferencing features in the map such as the hydrology network, major road junctions and other landscape features to satellite imagery in a similar way. But what projection and coordinate system were they using? Notice that the lines of longitude are converging towards the south. This is a projection used for displaying entire continents known as "Azimuthal Equidistant"

1. Open Arcmap and right-click the "Layers" command and choose Properties... Under Coordinate System Choose Predefined > ___ (under construction...)
2. Add Data and browse to the scanned map JPG. Note that if you see "Band 1, 2,3" you've browsed in too far. Go back out one level, select the JPG file and choose "Add Data".
3. Choose View > Toolbars > Georeferencing…
4. You should see the map somewhere on the screen, if now choose Georeferencing... > Fit To Display. Next, using the Magnifier zoom into the lower right corner of the map. Note that "Azimuthal Equidistant Projection" is indicated under the title.
5. Choose the red/green plus icon in the Georef toolbar. and Click the 50/20 lines where they cross, then instead of clicking again (visual georeferencing), right click and type in -50 and -20 (which one is the X axis value? Hint: the X axis conventionally measures change in value from left-right or west to east).
6. Right-click the JPG title in the Layers and choose "Zoom to Layer" and then use the Magnifier to zoom into the top left corner where 80 and 10 lines cross, right click and type -80 and 10 into the fields. Why is the longitude 10 and not -10?
7. Then do the upper right and lower left. When you have completed four links, choose Update Display from the Georeferencing menu.
8. Click the Link table (right of the red/green plus icon) and you see the results. Notice the RMS error value for each value. You want a low residual error. The Root Mean Square (RMS) for the whole image shows at the bottom of the Georef info window.
9. When you are done, click “Update Georeferencing”.

Note that there is a lot of error in the result. These are shown as blue Error lines in Arcmap. Perhaps we should have georeferenced this map to a Conic projection. There are helpful resources online for learning about map projections. These include

• Peter Dana: The Geographer's Craft
• ESRI: Understanding Map Projections (PDF)

As you'll see in the exercise below, it's much easier to georeference GoogleEarth imagery because the latitude/longitude graticule consists of right-angles. It is a flat geographic projection.

PART II. Your Study Area

Acquiring and Georeferencing data for your study area.

A. GOOGLE EARTH IMAGERY

Visit the area in GoogleEarth (download free GoogleEarth installer, if necessary) and georeference data using these instructions

1. Setup: Using GoogleEarth 4-beta choose Tools > Options… and use these settings.
   Detail window size = Large, Lat/Long = Degrees (not Deg/Min/Sec), Quality relief = Max, Anisotropic filtering = Off, TrueColor, Label Size=small. Terrain Quality = Higher, Elevation Exaggeration = .5
2. Zoom into the high res image location. I've found that 700m (2300') "Eye Alt" was optimal for my study area in rural Peru (I think it's 70cm data). Make sure your viewing angle is nadir. Turn off all the screen stuff possible (compass, sidebar, status). Just the minimum toolbar and the logos.
3. Turn on Lat/Long graticule, click "Save As... JPG" and name it "FilenameLL.jpg". Do not move your view at all. Turn off Lat/Long graticule and repeat: "save As... JPG" as "Filename.jpg" for a second file.
4. In Arcmap (WGS84/Decimal Lat/Long geographic projection) georeference "FilenameLL.jpg" with the Lat/Long grid using the graticule intersections. Make sure the "Auto Adjust" command is checked in Georeferencing menu. You can enter values numerically for the "Georeference To..." graticule by right-clicking. When 4-5 points are referenced use "Update Georeferencing..." in Arcmap to write out the worldfile and AUX file.
5. In Windows go to the folder and duplicate and rename these two files:
   "FilenameLL.aux" to "Filename.aux"
   "FilenameLL.jgw" becomes "Filename.jgw"
6. Add the layer "Filename.jpg", it should line up exactly with the LL image.

Finally, as part of this assignment:

• Draw a Polygon bounding your study area in Latitude / Longitude space. Use the techniques we used in Class 1 (remember digitizing the pyramids?) in order to create a bounding box.
• Save this file in a good place, you'll reuse it.

Incidentally, with ArcGIS 9.2 the GoogleEarth vector format (KML) is supported for direct read/write from within Arcmap.

B. TOPOGRAPHY

1. Next, we will acquire topographic data for your study area from the SRTM data (CGIAR).

Instructions for converting GeoTIFF DEM data to GRID (for both SRTM and ASTER DEM data)

• Acquire SRTM data a GeoTIFF, Export... Export to GRID format, then reformat with the following command in Spatial Analyst under Raster Calculator:

setnull ( [GRIDNAME] < 0 , [GRIDNAME] )

That command sets all topographic values less than 0 (sea level) and the no-data collar area to <NULL>.

If your study area is on the edge of various tiles you can merge them into a single large GRID by using the following method:

Zoom out to show the whole study area and go to "Options..." in the Spatial Analyst, choose "Extent" tab, and scroll the list upward to "Set the Extent to the same as Display".

Return to the Spatial Analyst > Raster Calculator and do this

mosaic ( [GRIDNAME1] , [ GRIDNAME2], [GRIDNAME3] )

with as many grids as you need.

2. To get topographic data that is 30m (3x higher resolution than SRTM), try to acquire topographic data from ASTER. The problem with ASTER is that it is from individual satellite images and so there are a lot of edge issues, and also any clouds will appear as big holes in your dataset. However, ASTER is probably the best free DEM layer you'll get in less-developed nations of the world, and you also can get a 15m resolution satellite image that registers perfectly to the DEM for further analysis. It's definitely worth the time searching for ASTER imagery.

To be clear: by locating a cloud free ASTER scene you can get both 30m DEM (topography) and 15m multiband imagery from that particular scene.

• In the menus set the Sensor menu to ASTER... VNIR, and in Resolution zoom into your study area at 400m resolution.
• Under the Map Layers menu you can turn on boundaries, roads, and other layers that may help with orientation.
• By right-clicking you can send cloudy images to the back until you find a cloud-free image on your study area. You can also filter out cloudy scenes using the "Max Cloud" filter level on the left side of the screen.
• Try to find sequences of images from one overflight. Click "Next scene" and "Prev Scene" buttons will reveal these swaths, and you'll note they come from the same date. These swaths stitch together really well into a larger DEM.
• Send me the file name (it starts with L1A) and I will work on ordering these files for research.

ASTER DEM arrives as GeoTiff and it can be converted to GRID using the same instructions mentioned above (section B1) for SRTM data.

ASTER imagery processed to the L1B level and acquired in a multiband format called HDF-EOS Swath. The HDF format can not be directly imported into ArcGIS but you can convert these filese to GeoTIFF using free software following the directions posted here.

C. MULTISPECTRAL IMAGERY

Visit the Univ of Maryland data depot and acquire a scene of Landsat TM+ imagery for your area using Map search.

• Check the ETM+ box for Landsat Thematic Mapper+ data and click "GeoTIFF" in the Require box at the bottom.
• Zoom in closely to delimit your study area (dashed box above the map) and click "Update Map" to find out how many images are available in that area. Download as GeoTIFF.
• On the Download page look for the series of images that are Bands 1 through 6 with file names that end in B10, B20 or something like that. Download bands 1 through 3. Unzip and Add the GeoTiff to your Arcmap project.
• In Toolbox use Data Management > Raster > Composite Image... to combine these three images into a single image.
• Use Symbology to reassign the bands so that Band 3 is Red, Band 2 is Green, and Band 1 is Blue.

D. Global Vector data: VMAP0 and VMAP1

Some countries serve geographic datasets online and you may download these from government-specific servers. For example, there are many datasets for regions in the United States on federal and state GIS servers and the European Union serves a variety of datasets online as well.

Research taking place in other countries will find that policies vary widely for two principal reasons. First, in the case of many less-developed countries, there may be few detailed digital data available for the public. Secondly, many countries have strict copyright restrictions on government data and serving those datasets on line for reuse in a GIS and maps for publication would violate copyright laws.

In these cases, global datasets like the raster data presented above and a few global vector data sources, are particularly valuable. Vector data at 1:1 million and 1:250,000 scale are available in the public domain from an older US Government project known as Vector Smartmap (VMAP).

The official server for VMAP data is NIMA's Raster Roam server, however it is easier to acquire VMAP0 and VMAP1 datasets from MapAbility.com. These data are in WGS84, decimal degree. ArcGIS can read the VPF format directly and you can save them out as Geodatabase or Shapefile.

You can download the VMAP0 level data on a country by country basis, rather than in large tiles, at the Digital Chart of the World.

The less-detailed VMAP0 data is largely consistent with the ESRI World dataset that you may have on your computer. The 2006 edition of ESRI Data and Maps comes on five DVDs with the global SRTM topographic data set included.

There have been efforts to get the US Government to release the entire VMAP1 dataset because it is not technically classified (it is "limited distribution") and as an unclassified, tax-payer funded project there is an obligation to release the data under the Freedom of Information Act.

Other useful sources of free geographical data are indexed online at websites like GlobalMapper. Searching the web with terms like your geographical area and "shapefile" can sometimes turn up useful project-specific datasets served online.

E. Give credit for these data

These US Government data are in the public domain, but in publications and websites using these data you should include a line thanking the source. It might read something like this

"We want to thank NASA and JPL for allowing the use of their ASTER and Landsat Images."

 

Week 4 - Queries, relates, and buffers

Classroom Topics

Further discussion of database normalization and relates, overlays, buffers, and other means of working with GIS data in a relational database structure.

In class presentations.

In-Class Labwork, Week 4

Manipulating data through queries, overlays, and other methods become more complex with relational databases, but understanding how to work with these data is fundamental to organizing a project in digital structure.

1. Linking related tables through primary key with a spatial index

We learned that anthropological data often involves working with data in related tables that are linked (Joined or Related) through unique ID numbers. The theory behind design of relational databases is known as Database Normalization.

When detailed data is held in non-spatial tables (from lab analysis, for example) it can be difficult to connect the data in these attributes tables back into physical space for analysis and mapping. Recall that we used a Primary Key (ArchID) for indexing all spatial proveniences and then a CatID key for individual artifacts within those spatial areas.

The ArchID Centroid solution

One expedient solution for assigning space to non-spatial attributes is to have a single point type feature that contains a single point for every ArchID number regardless of whether it is the location of a locus of ceramics inside of a site (a polygon inside a site polygon), an isolated projectile point (a geographical point), or a single core at a site (point inside a polygon). All ArchID numbers are reconciled in a single point feature class and therefore space can be assigned to every item in some form and all these non-comparable attribute tables can be effectively “zipped together” into space.

What about the artifacts collected from line and polygon features? How do you mix spatial location for points and polygons into a single file? For the purposes of organization, you can turn lines and polygons into centroids. Centroids are defined in a number of ways, but think of them as the center of gravity for a line or polygon. In the Callalli database the All_ArchID shapefile is a collection of point locations and centroids for all of the ArchID numbers from the Callalli area. Keep in mind that a number of items with different CatID (from lab work) can be assigned to a single ArchID (hence, a single point), and that there are a number of limitations to using centroids for analysis.

This method is a solution for dealing with the “Many to Many relationships” situation.

 

Queries and related tables in Callalli data

 

If you don't already have it, download, unzip, and load the data from the Callalli geodatabase.

Part A. Query and display relates

Quick exploratory task: Make a map showing the locations of all obsidian bifaces and projectile points because we want to know if they are close to rivers.

One possible solution to this task is as follows

• Open Attribute Table for non-spatial table “Lithics_Lab2”
  

Look at the data organization. As this is a non-spatial table it may not appear in the Table of Contents unless you have the “Source” tab selected at the bottom of the list.

The two major problems are:

1. These are non-spatial, so how do you show them on the map?
2. The attributes are spread across two fields so how can you easily select them for display?

Take a look at the Attribute table for the ArchID layer. This is derivative feature containing centroids for lines and polygons, and point locations for all instances of each ArchID field. Look in the table and notice that it’s a Point type geometry file with a single Point record for each ArchID. The “Filetype” field tells you what file type the original ArchID number belongs to so we can relink these centroids to their original polygons if needed down the road. Also notice the PhotoURL field contains links to site photos. We’ll explore that in the future.

We need to link the table “Lithics_Lab2” with All_ArchID points… but there are many Lab results for each ArchID so we can not use the JOIN function because this is a one to many (1:M) situation.

Instead we will use the RELATE command

• Right click All_ArchID and choose Joins and Relates… > Relates…
• Read the description and then use these values in the Relate box:

1. ARCHID
2. Lithics_Lab2
3. ARCHID
4. type in “ArchID-LithLab2”

 

Now we need a selection in the Lithics_Lab2 table.

 

• Open the Attribute table for Lithics_Lab2.
• Right-click Lit_Mat field and choose Sort Ascending
• Scroll down until you get to the Obsidian artifacts and click and drag down in the left-most column to select these records. Now all Obsidian artifacts should be highlighted. The next problem is that we only want some of the obsidian artifacts.

 

Another way to make or modify a selection is as follows

• click Options.. at the bottom and choose “Select by Attributes”. We can use this box to do a modified SQL query of the table. In the Method field choose “Select from current selection”.
• Double-click [Form] and notice how it pops up in the text box below. We’re going to build up an SQL query using graphical tools. Click “=” then Click “Get Unique Values”. From this list double-click “Biface Broken”. Click “OR” then click [Form] and ‘=’ again, then choose “Biface”, then repeat these steps adding “Proj Point” and “Proj Point Broken” to your selection criteria.
• Click the Verify button. Did you pass the test?

Your line should look like this

[Form] = 'Biface Broken' OR [Form] = 'Biface' OR [Form] = 'Proj Point Broken' OR [Form] = 'Proj Point'

• Click “Apply”

You’ve got a subset of the table. Notice the number of artifacts that are selected. Now in order to see these geographically we need these features selected in the All_ArchID point layer.

• Click on the Options… button and go to “Related Tables…” and choose AllArchID-LithicsLab2.

The All_ArchID attribute table will appear with only those records selected that are contain obsidian bifaces and proj points. How many are there? Many fewer, what happened to the number of records highlighted in the previous selection?

Close this attribute table and you will see on the map that those point locations are highlighted. Are they close to rivers?

In this part we learned that a single point feature (All_ArchID) can be used to give geographical position to non-spatial tabular data provided that they have some reference to spatial data (such as a unique ARCHID number). Through the use of Relates and linked through a common reference table the All_ArchID table links different data sets using space as a common referent. You can quickly create selections in one dataset and move that selection into other datasets. Think of the All_ArchID table as the spinal column that links different elements of the skeleton.

Note that we used two methods of querying: the first was to just Sort Ascending for a particular field and select from that group. The second was to use text-based queries to construct an explicit query. For simple selections the first method is easier, but for complex queries, non-contiguous groups, or to store the query for later reference the latter is better.

Keep in mind that All_ArchID is only centroids so they don’t have the full information of the original points, lines, and polygons. However, this single spine can be used to jump between related selections.

For example, if we Relate All_ArchID to the Sites_A field we could find out the size of the sites that have obsidian bifaces. Are the sites with obsidian predominantly large or small sites?

 

Lets try that. Without losing your previous selection,

• right-click All_ArchID and choose Joins and Relates…> Relates… and for relates use

1. SITEID
2. Site_A
3. ARCHID
4. call this “All_ArchID-Site_A”

• Now right-click “AllArchID” and go to the Attribute Table.
• At the bottom go to Options… > Related Tables… note that you now have several Relates to choose from. Choose the one to Site_A.

• Now look at the Site_A attribute table. How many sites are selected? Notice how our selection is getting smaller as data is aggregated into these inclusive groups such as Sites.
• Click the Selected table at the bottom of the screen. You can see that the Shape_Area field shows the m2 of these sites. A frequency distribution on site sizes can be found by right clicking the Shape_Area field and choosing “Statistics…”.

These techniques, combined with Pivot Tables and Joins that you learned in labs during weeks 1 and 2, give you the basic tools to explore and manipulate data in databases organized through relationships. One of the advantages of using the ESRI Geodatabase instead of the older Shapefile format is that you can build permanent Relationships directly into the geodatabase so you don’t have to recreate them for each Arcmap MXD project.

There are still some cumbersome elements to related tables organization, for example symbolizing and labeling through relates is still not easily available in Arcmap. However with clean data organization you can move through joins and relates to produce special joins for specific map projects that require this kind of symbology.

 

 

PART II – Buffers

Buffers are extremely versatile in GIS. They are commonly used for expanding or contracting a polygon by a constant value, however they can also be used other useful functions. For example, you can use buffers convert points and lines into polygon areas (corridors). You can use buffers to evaluate spatial proximity from one theme, like a road, on another theme, like an archaeological site.

Exploratory question: what is the relationship between the presence of obsidian in sites and the proximity to rivers in the Callalli area?

We will use the “Obsidian by Site” table you created in Lab 2.

Recall that this table aggregated lithic locus data to by site in order to compare the density of obsidian and non-obsidian by site.

There are numerous ways to calculate distances in Arcmap. We will explore two methods today.

1. Multiple Buffers

• Buffer the rivers by opening to the red Toolbox icon choosing Analysis Tools > Proximity > Multiple Ring Buffers…
• Input Features: choose rivers in “Hydro_lines100k”
• Output Feature Class: hydrobuff (specific your output location by clicking the Folder icon)
• For distances use 25, 50, 250, 500, 5000 (click the Plus between each one).
• Click Ok.

The Obsidian_By_Site table is a-spatial so you have to Join that table to a spatial table. Let’s use All_ArchID because we know that every value in the Obsidian_By_Site table will have an entry in the All_ArchID point file (can you think of any problems with using points instead of site Polygons for this analysis?)

• Right-click “All_ArchID” and choose Joins and Relates…. > Joins

1. SITEID
2. Obsidian_By_Site table
3. SITEID

• Then click Advanced… and choose “Keep only matching records…” (why are we doing that step?... read the text. This is an exclusive, inner join)

Now we need to know where these features fall with respect to the hydro buffers layer underneath it. Use the toolbox Analysis Tools > Overlay > Identity… to compile all the attributes from the two layers into a point layer.

Use All_ArchID as the Input Feature and HydroBuff as the Identity feature. Click OK.

Look in the attribute table of All_ArchID_Identity” and notice you have a DISTANCE field (distance from river, by buffer class) and Site_Sum_Obsidian. These results could be explored numerically (is there a meaningful relationship?), or they could be symbolized together.

• For example, right click “All_ArchID_Identity” and choose Symbology.
• Show: Quantities, Graduated Colors.
• Value: Site_Sum_Not_Obsidian
• Normalization: Distance

Quantitative Proximity Distance

What if you want to know the actual distance in meters between a point and the river, and not the grouped buffer class of these distances? For this we need to use the Raster data model (continuous values).

 

• In the Toolbox choose
• Spatial Analyst Tools > Distance > Euclidean Distance…
• Input Raster/Feature: Hydro_lines100k
• Cellsize: 90
• Click OK

What happened? Zoom to Layer of the output layer (EucDist_hydr2).

Look carefully at the classes produced. Those are JUST for visualization.

• Under Spatial Analyst toolbar choose “Zonal Statistics…”
• Zone Dataset: All_ArchID_identity
• Zone Field: All_ArchID_ARCHID
• Value Raster: EucDist_hydr2

Have a careful look at the a-spatial output table (by default its called zstat) and see if you understand the results.

Note that the Value field is ArchID. That means you can use a Join to connect All_ArchID to the zstat table and connect the output table to spatial locations through that join.

Again, these can be symbolized or explored numerically.

 

Week 5 - Raster Data Model: DEM and other continuous data

Exercises:

• Local Scale Rasters
• Brief visit to ArcScene
• Hillslopes and Topographic DEM
• Cartography with DEM
  

Classroom Topic: Introduction to Rasters

Continuous data is represented in the form of cellular or “gridded point” in a GIS. This data model is suitable for working with themes that consist of continuous values across spaces. Examples include: elevation, vegetative cover, temperature, and barometric pressure.

In archaeological applications a raster theme might include all artifacts of a particular class, such as obsidian flakes, across a space, or all the occupation areas from a particular time period. Generally the rasters are thematically simple: one attribute value is shown varying across space. Data is organized logically into layers or surfaces. With Raster data we are moving beyond the simple data management, cartographic applications of GIS into the more interesting realm of theoretical and analytical problems that you could not accomplish without a computer.

You’ve already worked with Rasters in this class in previous labs. The GoogleEarth and imagery, the Landsat scene, and the SRTM elevation data were examples of raster data.

In-Class Labwork, Week 5

Working with raster data is less intuitive than vector data for many users. This exercise works with two different scales of raster data.

PART I: Local level raster data

1. Load vector data sets.

• Start a new map in Arcmap and load two themes from the Callalli geodatabase.

1. Site_A: the site boundary polygon. For the purposes of this demonstration all the sites in Site_A have a minimum density of 1 flake per square meter.
2. Lithic_A: the lithic locus polygon. Here the density is determined from the C1_DENS field. Low = 3 flakes / m², Med = 7 flakes/m², and High = 15 flakes/m².

You should write down these densities for later reference below.

• Display the data layers by bringing in both feature classes with Site_A underneath Lithic_A.

• Display Lithic_A using a density choropleth: Right-click on Lithic_A > Properties… > Symbolize and choose Show: Categories, Unique Values. Value Field: C1_DENS. Click “Add All Values…” at the bottom. Change the colors if you want.

These data were gathered using a Mobile GIS system. With the GPS running I walked around different densities of artifacts I perceived on the ground.

2. Convert these data to Raster

• Make sure nothing is selected and go to Spatial Analyst toolbar > Convert… > Features to Raster…

Input Features: Lithic_A
Field: C1_DENS
Output Cell Size: 1 (meter)

Output Raster: <click the Folder and go to your /callalli/ work dir and create a new folder called “Lithics”. Save this raster called “LociDens” into /callalli/lithics/

We want to repeat this operation with the Site_A data, but as these are not lithics-specific (they are merely site boundaries) we need to prepare the Site_A file for conversion to raster.

• Open the Attribute Table for Site_A (Right Click… Attribute Table)
• Choose Options > Add Field… at the bottom of the table
• Create a Short Integer field named “DENS”
• Now fill that column with the density (per m²) of the Site_A raster value mentioned above. Back in the Attrib table right click the field heading and choose “Calculate Values…” and then type in the value (1) of the density per m² for the Site_A in the DENS= field.

Now you can create a Raster with the DENS value using the Convert Features to Raster… technique you just used with the Lithic_A field. Save it into the /callalli/lithics/ folder under the name “SiteDens”

You’ve just created to different Raster files from GPS derived Vector polygon data.

Let’s change the Vector data layers to thick hollow outlines and put them on top so you can see how the Vector was converted to Raster. Zoom in close enough to see the raster resolution.

• Zoom in extremely close so only a few grid squares fill the screen
• Get the ruler tool and measure the size of the grid square.

It is a good idea to check rasters in this way to confirm that you have gotten what you expect.

3. Reclassifying the Locus raster

• Look at the Loci values in the attribute table. We want these Locus values to reflect the m² lithic density as well. We will use the Reclassify command to change these values into m² values that we want.

• Go to Spatial Analyst > Reclassify…

• Type in new values for 1,2, and 3. Recall that 1 = High density, 2 = Med density, and 3 = Low density. The actual m² values were mentioned above: Low = 3 m², Med = 7 m², and High = 15 m². The default results in a temp GRID file called “Reclass of LociDens”, which is fine for now.

4. Combining the GRID files

Now we want a single continuous surface from the Site and the reclassified Locus GRID files.

• In Spatial Analyst > Raster Calculator…. Use the Merge command to put these two rasters together.

The format is

MERGE ( [GRID1] , [GRID2] )

and so on, substituting the GRID names for GRID1 etc. In this case, GRID1 should be "Reclass of LociDens and GRID2" is "SiteDens"

Unlike the Mosaic command you used previously, the Merge command does NOT blend the GRIDs together and the cell values remain discrete. Also, the order of the GRIDs in the list is important, so the GRID1 is on top of GRID2 in the output. Since Sites are bigger than Loci spatially, we want SiteDens at the bottom.

Notice that what you have is a single raster surface representing a theme "Lithic density" from different GPS derived files. The cells themselves are 1 m² and the value of the cell is the estimated density of lithics found in that square area.

If you’re satisfied with the output we need to save this file in a good place. The output of your raster calculator command is a temporary GRID file called “Calculation”. Since we are Make this a permanent file, right-click > Make Permanent…. And put that file in the /callalli/lithics/ and call it “LithicDens”.

Save this file. We will work with it further in the coming week.

5. Some words about working with Raster data in ArcGIS.

GRID files are often single band, but they can be combined into a Multiband grid. Thus you could have Chert and Obsidian lithic layer separated into different GRIDs but stored together. We used the Combine Bands command in Week 3 lab to combine Landsat bands that were stored as individual GRID files into a single larger R,G,B file. This command is an update of the GRIDSTACK command.

GRID files are an internally compressed binary format that is the native Raster format for ESRI products. Often transformations of other Raster formats that ArcGIS supports, such as TIFF, JPG, IMAGINE (IMG) require converting each band separately into GRID files and doing the operation, such as reprojecting to a new coordinate/datum, and then re-combining the GRIDs.

GRID files do not always behave as you expect because it is an old format that doesn’t necessarily comply with the Windows file explorer.

Here are some hints for working with GRID files.

- keep file names short and try to avoid having any spaces in your paths. This means “My Documents” is out because there’s a space in the folder name, and there are also spaces earlier in the path as well. Often people will work in “C:\GISDATA\” or something simple like that. ArcGIS9 is better at handling spaces in GRID filenames, but it is still best to avoid this practice.

- Look at your GRID files in Windows Explorer. Browse to My Computer and locate your data and look in the folder where your raster is located. There is a folder named for the GRID, but there’s also an “info” directory and a .AUX file. The point is, this isn’t a normal file system format and you can’t move GRIDs in Windows! Use ArcCatalog to rename, copy, and delete GRID files.

- It is important to be tidy and under control when working with GRID files because they can be very large. You don’t have space to store mistakes and mix them with good data. Pay attention to where you’re saving files and as soon as possible (before finishing for the day) go back and clean up the experimental junk files and the files from intermediary steps that inevitably result from working in Spatial Analyst.

- keep GRID files segregated into their own folders whenever possible. This makes it easier to deal with GRID files later because they don’t share an info directory. You CAN move GRID files, zip them, copy them around in Windows as long as you take their enclosing folder and you don’t touch the stuff next to the info directory. If you see an info directory, don’t touch anything associated with GRIDs in that folder.

- Finally, Spatial Analyst creates a lot of Calculations and these are stored in the TEMP folder that is specified in Spatial Analyst > Options… You don’t want to leave your stuff as Calculations in this class because they will get wiped off the drive. Right Click all the Calculations you want to save and choose Make Permanent… and consider putting them in their own folder!

---

PART III. Cartography with DEM topographic data

The DEM data you acquired from SRTM can be used cartographically for representation of the land surface, but it also forms the basis for a number of analyses that you may compute.

Lets say we're designing a project where we need to ignore all slopes over 15 degrees because it is too steep for the features we're looking for. How do we delimit those areas?
1. Calculating slopes:

• Load the Callalli DEM file and put it at the bottom of the layer stack. Make it a nice Dark brown to Light brown (yellow) symbology gradient using Stretched symbology.
• Go to Spatial Analyst > Surface Analysis > Slope…
• Choose Input Surface: Callalli_DEM
• Output Measurement: Degrees or Percent.
• (hint: a 100% slope = a 45 degree slope. I prefer to work in degrees, but many engineers use %).
• Leave the defaults and Click Ok. Look at the result. Do you understand what the colors mean?

2. Choose Spatial Analyst > Reclassify….

• Input surface: Slope of Calllalli_DEM (Note: Thats SLOPE OF...)
• Click Classify. Choose Classes: 2.
• There are two values on the rightmost column. Change the upper one to 15.
• Look at the histogram. Do you understand what is going on?
• Click OK. Look at the Old > New Values. See how we're making two types of slope?

3. Choose Spatial Analyst > Convert > Raster to Vector…

• Choose Reclass of Slope of Callalli_DEM. Use the defaults.
• Now symbolize the output so that the slopes over 15 degrees have a line hashuring through them and the other polygon class is unsymbolized.
• Put this above the Topography layer. Does it seem to make sense with the topography?

---

PART IV. Representing DEM data

1. Hillshade - cartographic

• Using the Callalli DEM file create a Hillshade using Spatial Analyst > Surface Analysis > Hillshade…
• Use the default settings for now. Call the output file "callalli_dem_hs"
• Put the Hillshade file above the DEM file in the layer stack.
• Set the Hillshade transparency to 50% under Properties… > Display…
• How does it look?

Note that these data are Z values in meters on in a UTM coordinate (metric) horizontal space. When you work with SRTM data chances are it'll be in Decimal Degrees horizontal units, but metric Z (altitude) units. Because of this inconsistency, use a Z factor of 0.00001 when producing Hillshades from a Lat/Long DEM such as your SRTM dataset.

2. Add contour lines

• Spatial Analyst > Surface Analysis > Contours…
• Make sure the Input Surface is Callalli_dem. Choose a contour interval of 25 (what units are these?). Save the file as Contour25 in the /callalli/ folder.
• Add the rivers layer. Do the rivers line up properly with the contours? This is an important check of the registration between hydrology and topography because rivers always flow down hill.

3. Highlight and label index contours.

Cartographers usually have bold contours at regular intervals to help the eye follow the lines.
Zoom out so you can see most of the study area. Open the Attribute table for the Contour. Notice how each contour line has its own row with CONTOUR indicating the metric elevation? Select a few of them and see them get highlighted on the map.

• In the Attribute Table choose Options… > Add Field… and create a field called INDEX and make it short integer.
• Choose Options… Clear Selection so nothing is selected. Then choose Select by Attributes…
• In the selection dialog box use the following code:

MOD( "CONTOUR" , 100) = 0

Do you understand what this query does? Modulus is the remainder after a division operation. Thus, this query selects the contours that can be evenly divided into 100.

• When you have the 100 interval contours selected, close the dialog box.
• Right-Click Index and go to Calculate Values…

You want it to read: [index] = [CONTOUR] for the selected rows.

• Now you have the Index contours selected out and you can symbolize and label using them.

4. Label just the Index Contours

• Right click the Contours25 layer and choose Copy, then go to the edit menu and choose Paste.

You'll have two copies of Contours25. Rename one of them Contours100.

• Go to Symbology for Contours100 and choose
• Show: Categories, Unique Values. Value Field: Index
• Click "Add All Values". Now click the 0 value and Remove it.
• Click on the top line, shift-click on the bottom line so all the values are selected. Right click and choose "Properties for selected symbols". Now make these 1.5 width and a dark color. Click Apply, how does it look?
• Go to the Properties > Labels tab. Check Label features in this layer.
• Method: Define classes. Click SQL Query…
• Use index > 0 as your query. This allows you to label only the Index contours.
• Click Label Field is CONTOUR. Click Placement Properties and put them on the line. Make the font Bold.
  

How does it look? See if you can put a MASK behind the contour in Symbol > Properites > Mask… then set the white Halo to 1.5

• Save your MXD file.

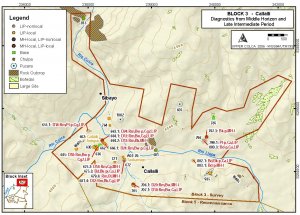
Click map to see a topo map (diagnostic ceramics theme) for the Callalli area from my dissertation.

 

Finally, this week the task is to use these techniques to develop an attractive topographic map for your study region using your SRTM data.

 

Week 6 - Points and pattern analysis

Week 6 In-Class Exercises, Points and pattern analysis

• Random point generation for Stratified Cluster Sampling
• Analyses of Point Pattern Dispersal

PART I. Random samples and point pattern analysis

A. Download and Install Hawth's Tools for statistical analysis

We will use a third party tool to generate random sampling locations. There are thousands of useful scripts and tools for ArcGIS that you can download for free from

http://arcscripts.esri.com/

Go there now and change "All ESRI Software" field to "ArcGIS Desktop".
There are many other useful tools on Arcscripts for completing a variety of tasks. It's often a good place to go to extend the capabilities of ArcGIS.

Search for "random points" and you'll get half-dozen tools related to this function.
Download Hawth's Analysis Tools for ArcGIS 9 by Hawthorne Beyer

Don't download it from the Arcscripts site, however, because it is out of date on there (as he notes on the webpage). Click on the "www.spatialecology.com/htools" link and get the latest version from there.

Download and unzip Hawth's Tools to a folder, and install it by double-clicking on "htools_setup.exe"
Use all the default settings during install.

Open Arcmap and right-click in the vacant space on the toolbar area and select "Hawth's Tools" from the list. A small window button will appear, drag that into an open position on your toolbar.

B. Cluster sampling for Fieldwork

In order to evaluate the strength of a particular spatial distribution many spatial analysis techniques will compare a known distribution to a randomly generated sample of point locations. We will use random sampling methods in two applications.

1. For collecting samples in the field we will have the GIS generate a number of random point locations for sampling in a polygon feature where the size of the sample (by count) is relative to the area of the feature being studied.
2. We will use randomly generated point scatter to learn about the point density spatial analysis tools in ArcGIS.
   

The issue of spatial sampling is more involved than we have time to go into today. For further reference in sampling in archaeology please see

Banning, E. B. (2000). The Archaeologist's Laboratory: The Analysis of Archaeological Data. Plenum Publishers, New York. Pp. 75-85.
Drennan, R. (1996). Statistics for archaeologists: A commonsense approach. Plenum Press, New York. pp.132-134.
Shennan, S. (1997). Quantifying archaeology. Edinburgh University Press, Edinburgh. Pp. 361-400.

How big should a sample size be? There is no fixed rule about proportionality of the size of samples because sample sizes are determined by the variability (standard error) of the phenomenon being sampled and the desired statistical strength of the results.

• In this exercise we will use Site_A and the DEM from the Callalli data so Add those to your project.

In this example we want to collect artifacts within 1 m² area of sample points from all the archaeological sites based on area (m²) of the sites. In order to implement this we would use a GPS to guide us to these sampling locations in the field. This is a type of Cluster Sampling because you will collect all artifacts within a particular 1m² collection location.
If we want a circular area that is 1 m² we can either try to make a box with measuring tapes, or we can use the dog-leash method and delimit a circle that is 0.56m in radius. Since the area of a circle is pi*r² then
r = sqrt (1 / 3.1415) and therefore r = 0.56m

Thus the most expedient way to do this is to navigate the sample locations selected below and for each location draw out a circle 56 cm in radius and collect every artifact in that circle.

• Open the Attribute Table for Sites_A.
• Options > Add Field…
• Add an integer field called "Samp"

Look at the value in [Shape_Area]. Because this is a Geodatabase feature (as opposed to a Shapefile) the Shape_Area field is generated automatically and always up-to-date.

Scroll quickly down the list. What are the largest and the smallest sites you see? We want to sample a little bit from the small sites, and proportionally more from the larger sites.

Here is one possible solution.

• Right-click "Samp" and Calculate Values…
• Use this formula: Log ( [Shape_Area] / 10 )

We are taking the Logarithm of what?

Note that the output is nice round integers (good for sampling) and not decimal. Wouldn't you expect decimal values from the Log calculation above? It's because the Field type was Integer so it rounds the result to whole numbers.

Note that one of them is a negative value, which isn't great, but it's a very small site so we can consider not sampling it.

Now we can run Hawth's tools Stratified Sampling methods using the samp values.

• Go to Hawth's Tools > Sampling Tools > Generate Random Points…
• Click the "Web Help" button at the bottom and skim through his description of the tools.
• Select Layer: Site_A
• Enforce Minimum Distance between points: 2
• At the bottom of the page choose "Generate number of points per polygon specified in this field:" and choose "samp"
• Once you've done that you need to go up to "Polygon Unique ID Field" and choose ArchID from that list.
  
• Output the sampling points to a file called "Sites_Rand1" in the Callalli folder.

Look at the "Sites_Rand1" attribute table and notice that each record has an ArchID value linking it to the site # in question. This could be very useful when you're actually navigating to these sampling locations. This will obviously be a one-to-many relationship with many samples from each site.

Zoom in to a single large site and look at the results. Is this a sample you'd like to collect? It would involve revisiting many places so maybe you would choose to sample from fewer sites instead based on further information about those sites.
There is a tool for mobile GIS work in Arcpad that allows you to construct a similar sampling strategy while you're still in the field. Thus you could do a cluster sampling method immediately while you're still at the site and not after-the-fact as we're doing here. In this case, you'd navigate to these point locations with GPS and dog-leash out a circle that is 56cm in radius and collect the contents.

A similar approach could be used, for example, to sample from the types of plants being grown in mixed cultivation farm plots. The study of Iraqi mortality since 2003 that we discussed also used cluster sampling methods because they would identify a neighborhood and then they would visit every household in a particular neighborhood. They used GPS in the 2004 method, but they used main streets and side streets to perform the sampling in the 2006 study which opened them up to criticism regarding bias in the sampling due to the dangerousness of main streets.

See Shennan (1997: 382-385) for more information on applying these methods to archaeology.

---

Part II. Point pattern dispersal studies

There are two basic categories of measures of point patterns dispersal.

1. The first category uses only the point location and the points are basically all the same characteristics they have only their spatial position to differentiate them. An example of this might be body sherds of a particular paste type scattered throughout a site or a region.
2. The second category uses some attribute, often numeric but sometimes non-numeric, that can be assessed relative to spatial location.

A. Spatial Structure for Point locations without values

In an example of this kind of analysis we might ask: is there spatial structure to the concentrations of Late Intermediate period pottery in the Callalli area?

The first basic problem is that we collected sherds into a variety of spatial proveniences: ceramic_point locations, sites, ceramic loci, even lithic loci in some cases. This is where the All_ArchID layer comes in handy. You'll recall that All_ArchID is a point layer showing the centroid of ALL spatial proveniences from our survey survey regardless of the file type. This is like the master record or the spinal column that joins all the various tables. However we still have a 1 to Many relationship issue with respect to getting point locations for every sherd. There are many sherds in one site, for example, and only one centroid to join the sherd location to in order to conduct analysis.

One way to solve this is to reverse-engineer a MANY-to-ONE join. This is not something that is done naturally in Arcmap because we're effectively stacking points on top of points, which is a bad way to organize your data. However for these particular analyses it can be useful.

1. Create a Ceram_Lab2_All_ArchID layer

• Load Ceram_Lab2 and load All_ArchID from the Callalli database.
• Recall that Ceram_lab2 is a non-spatial database so the Source table in the table of contents must be selected to even view it.
• Right-click Ceram_Lab2 and choose Joins and Relates > Join
• Use All_ArchID in field 2 then use ArchID for field 1 and ArchID for field 3. Click Advanced… and choose Only Matching Records
  

Why did we do that? Recall that we started with Ceramics data so this way we're ONLY including ceramics point locations.

• Go to Tools > Add XY Data…
• Choose "Ceram_Lab2_All_ArchID"
• And for X and Y choose "All_ArchID.X" and "All_ArchID.Y".
• For reference system choose Projected > UTM > WGS1984 Zone 19 S
• Look at the resulting attribute table in Ceram_Lab2_All_ArchID. There should be 113 records.
• Note that the file is "[layername] Events": it is not a regular Feature or shapefile. You must choose "Data > Export Data..." and save it out in order to proceed with this exercise. Export it to a Geodatabase Feature class (rather than a Shapefile) so that the long fieldnames will not become truncated.

We've now created a point layer that has one point for every diagnostic sherd we analyzed from this region. This occurred because of the directionity of the join. We broke the cardinality between 1:Many by reversing it so we got a ton of ONES and no MANYS. In oher words, all the MANYS are their own ONES, each with a point location. We can now look into the point location patterns.

2. Point structure for Late-Intermediate/Late Horizon period points

• Open Attribute table for Ceram_Lab2_All_ArchID and sort Ascending on Ceram_Lab2.Period_gen
• Select all the records that have LH as a value
• In the Toolbox choose Spatial Statistics Tools > Measuring Geographic Distributions > Standard Distance
• Choose the Ceram_Lab2_All_ArchID file as an input, for output call it CerLH_StanDist and leave it as one standard deviation.
• Run the operation and look at the resulting circle.

• Return to the Attribute Table for Ceram_Lab2_All_ArchID and choose just the LIP-LH rows and rerun the operation. Call the output “CerLIP_StanDist”.

Look at the two circles. What are these depicting? It is also possible to assign weights to these measures. The "Mean Center" tool, in the same area of Arctoolbox, will show you the mean center based on particular numeric values.

---

B. Point pattern distributions for points with values.

These analyses quantify the autocorrelation of points based on a particular attribute value.

Spatial Autocorrelation reflects Tobler's First Law of Geography where "All things are related, but near things are more related than distant things". We will examine this using a particular numerical attribute field.

In this example we don't have many numerical fields to choose from because not many quantitative measures were taken from these ceramics. We do have diameters from rim diameter measurements.

• Sort the Ceram_Lab2_All_ArchID table by "Diameter" and select only the rows that have values (hint: sort Descending). We could use Part:rim attribute to select these, but a few rims were too small to get diameter values for and so their value is empty.
  

Look at the distribution highlighted in blue. Do they look clustered or randomly distributed? Keep in mind that some points are stacked on top of each other from the Many to One stacking from earlier.

• In Toolbox choose Spatial Statistics Tools > Analyzing Patterns > Spatial Autocorrelation
• Choose the Ceram_Lab2_All_ArchID table
• Choose Ceram_Lab2.Diameter for the Field
• Check the box for Display Graphically
• Run the function
  

Study the resulting box. Does this confirm your visual impression of the distributions? The text at the bottom of the box shows you the proper statistical language to use when describing these results. This test is often used as an early step in data exploration to reveal patterns in the data that might suggest further exploration.

C. Cluster / Outlier Analysis (Anselin Local Moran's I)

One final analysis will display the degree of clustering visually and it produces standardized index values that are more easily comparable between analyses. This analysis displays clusters of points with values similar in magnitude, and it displays the clusters with heterogeneous values.

This analysis allows you to compare non-numerical values

• Unselect all records in all tables (go to the Selection menu and choose "Clear Selected Features").
• In Toolbox choose Spatial Statistics Tools > Mapping Clusters > Cluster/Outlier Analysis with Rendering
• For Input Feature choose Ceram_Lab2_All_ArchID table
• For Input Field choose Ceram_Lab2.Period_gen (note that these are non-numerical)
• For Output Layer save a file called Cer2_Per_Lyr
• For Output Feature save a file called Cer2_Per (note that these file names cannot be the same. If it does not run the first time try using different file names for the Output Layer and Output Feature)
• Run the operation
  

If the Red and Blue circles do not appear you may have to load the Cer2_Per_Lyr file manually from where ever you saved it.

These values are Z scores which means that the numbers reflect standard deviations. At a 95% confidence level you cannot reject your null hypothesis (of random distribution) unless the Z scores are in excess of +/- 1.96 (1 stan dev).
More information is available in the documentation and by the author of the geostatistics tool in an online forum.

Which points represent which time periods? Look in the Attribute Table and see which Field contains the Periods (LIP-LH, LH, etc). The field name is probably changed to something strange. Go to layer properties > Labels and label by the Period field name. Now you can see the homogeneous and heterogeneous clusters, and where they fall.

You're encouraged to read the help files and additional reading before attempting to apply these functions in your research.

 

---

Week 7 - Pattern analysis, Part 2

Week 7 In-Class Exercises, Pattern analysis Pt II

 

Comparing point patterns
This exercise will introduce functions found in the Geostatistical Analyst toolbar.

Introduction

The lab is organized around the following question in the Callalli data:

We know that obsidian is found about 15 km to the southwest of the area, but that chert cobbles are found in the local geology and the cobbles can be found in streambeds. We noted during fieldwork that chert artifacts are commonly found along the banks of the streams where there appeared to have been chert tool manufacture occurring. Obsidian appeared to be primarily located in discrete deposits that were imported from the source region.

On the principal of least effort we might expect that larger artifacts, particularly cores and concentrations of flakes, would be encountered close to the rivers in the case of chert but not in the case of obsidian. We could structure this in terms of hypothesis testing (H0: no relationships between weight of artifacts and proximity to streams; H1: concentrations of heavy chert artifacts are found in proximity to streams). However, a visual exploration of the relationship is also informative.

---

PART I. Point pattern exploration tools

A. Create study sets in Arcmap without altering original data table

• Download Lithics_Lab2_AllArchID.zip
• Unzip, add to project
  
• View the Attribute Table.
  

The Lithics_Lab2_All_ArchID table is constructed the same way as we created the Ceram_Lab2_All_ArchID last week. It is a de-normalized table where points were created for every artifact from our lab analysis using the best spatial provenience available.

Note that there are 390 artifact rows.

Look at the Attribute Table and observe the types of data involved. We have projectile points and other lithic tools, and a small sample of flakes. It turns out these flakes are only from a couple of sites, so lets exclude them. Also, we only want to work with Chert and Obsidian, so first we will select out the Chert non flakes using the Definition Query.

• Right-click Lithics_Lab2_All _ArchID and choose Properties... > Definition Query

• Try to construct a query that selects Chert from the Lit_Mat category and excludes cases where Form = Flake Complete, AND also it selects Lit_Mat = Chert and excludes cases where Form = Flake Broken.

• Build this query by clicking the buttons. You shouldn't have to type anything.
• Click Verify
  

Your query should look something like

("Lit_Mat" = 'Chert' AND "Form" <> 'Flake Complete') and ("Lit_Mat" = 'Chert' AND "Form" <> 'Flake Broken')

Build it yourself so you remember how… don't just copy that text!

• Back in ArcMap click the name of the Lithics_Lab2_All_ArchID layer and rename it: Chert_Tools (this set has cores in it too, but just call it tools for simplicity)
  

• Copy and paste the layer (right-click > Copy. Edit menu > Paste)

• Right-Click Properties > Definition Query
• Redefine this layer as Lit_Mat = Obsidian, but no flakes (same as Chert for Form).
• rename this layer Obsidian_Tools
  

Note that we can now work with subsets of that single table without altering the original table. How many records are found in each Attribute Table?

B. Spatially explore the table values by Frequency.

First, turn on the Geostatistical Analyst. This takes two steps

1. Turn it on under Tools Menu > Extensions… > check Geostatistical Analyst
2. Display the Geostatistical Analyst toolbar from your Toolbar (right-click blank area)

• Choose Geostatistical Analyst > Explore Data… Histogram

We have Coinciding Samples… Choose “Include All”.
Why do we have spatially coinciding samples?

• Select Obsidian Tools on the left field and Wt_g10 on the right.

• Look at the histogram. Note that frequency and weight are plotted.

• Click and drag a box over the right-most columns. What weight group do you think you have just selected?

• Look back at your map display and note the points that are selected.

• Open the Attribute table for the Obsidian Tools layer and click the “Selected” button at the bottom.

Note that you can interactively select by

1. spatial position in the map (using the blue selection arrow)
   
2. attribute characteristics from the table
3. frequency (histogram) of values in Explore window

This tool is very useful for data exploration and pattern recognition.

This display also allows you to include histograms as well as values like Count, Mean, St. Dev., etc. on your map layout (using the Add to Layout button) where you can also export them to PDF for use in Word documents, etc.

Part II. Mapping Clusters and Interpolating patterns

A. Cluster/Outlier Analysis: Anselin Local Moran's I

Apply the Cluster/Outlier Analysis function that we used in lab last week

• Make sure no records are selected in any layer:
• Selection Menu > Clear Selected Features
• Next go to Toolbox > Spatial Statistics > Mapping Clusters > Cluster / Outlier Analysis with Rendering…

Input Feature: Chert Tools…
Input Field: Wt_g10
Output Layer File (click the Folder and name it: ChertWtLyr1)
Output Feature Class (click the Folder and name it: ChertWt1)

• Run the analysis. Add the ChertWtLyr to the map if necessary.
• Run the same analysis again with Obsidian and call it ObsidianWtLyr1

Look at the patterns. Zoom and and investigate the red and blue dots. These are features with statistically significant autocorrelation (positive or negative).
The values are Z scores which means that the numbers reflect standard deviations. For example, at a 95% confidence level you cannot reject the null hypothesis (of random distribution) unless the Z scores are in excess of +/- 1.96 (1 stan dev).

• Return to the Geostatistical Analyst > Explore Data… > Histogram function
• Remember to Include All with Coinciding Samples.
• Back the map view select the high or low Spatial Autocorrelation areas with the Select arrow.
  

Look at those values in the Histogram and in the Attribute table. Can you figure out why they have high/low spatial autocorrelation values?

B. Interpolation with IDW.

The Geostatistical Analyst provides tools for examining these kinds of patterns in detail.

1. Geostatistics is premised on the concept discussed as the First Law of Geography: All things are related, but near things are more related than distant things.
2. The assumption in geostatistics is that groups of points that are the same distance and direction from each other will contain similar differences in the value of the variable (attribute) measured at those points.
3. Furthermore, geostatistics assumes that it is possible to predict through interpolation the values for unmeasured points based on their distance and direction from known points.
4. The semivariogram cloud is a graph that depicts the value differences between groups of points found at different distances from each other.

In this brief introduction we will simply produce an IDW surface using the default values and compare it visually to the known patterns.

• Geostatistical Analyst > Geostatistical Wizard….
• Choose Feature: ChertTools and Attribute: Wt_g10
• Next… Choose Include All…

We don't have time to explore all the feature here, but this window is concerned with the directionality and magnitude of the interpolation.

• Click the top-left button "Optimize Power Value". Click Next…

This window displays the interpolation algorithm and allows you to reject specific interpolated (predicted) values that diverge from the Measured values.

• Click Finish…
  

• The resulting display should be renamed "Chert IDW" and moved down to near the bottom of the map layers (so the rivers are showing, etc).
• Repeat the above process with Obsidian and Wt_g10

Study the results. Compare the Clusters/Outliers results (red/blue dots) with the geostatistical wizard output.

It is somewhat difficult to compare the concentrations of heavy chert and obsidian artifacts from these rasters because they obscure each other.

• Right-click the Chert IDW output and click Data… > Export to Vector…
• Repeat with Obsidian IDW.
• Color the contours lines different colors and you can really see the patterns.
  

You can compare the prediction strength in both layers

• Right click Chert IDW > Compare… choose Obsidian IDW on the right side. Note the different RMS errors.

There are other powerful interpolation tools in the Geostatistical Analyst including kriging and semivariogram production. If you choose to use these methods you should research the most appropriate interpolator for your task.
The Subset function is also quite powerful in Geostatistical Analyst. It allows you to set aside a portion of your data for validation purposes. We will use this function in the coming weeks in the locational modeling exercise.

Week 8 - Predictive Modeling

In class Exercise: Week 8

Predictive (Locational) Models

---

As discussed in class, predictive models range in complexity from a simple collection of landform criteria for planning efficient survey strategies, to complex logistic regression functions where the contribution of each variable is made explicit. As described in the readings, these various models can be categorized by three major elements: the types input data, types of output data (form of results), and goals of the model.

A simple Rule-based survey model can be constructed by assembling various criteria and progressively delimiting the terrain included in the survey. For example, one might survey all terrain in a river valley that is less than 500m from the highest river terrace, and slopes under 15 degree slopes. The construction of such a model in Arcmap would involve several Spatial Analyst operations.

First, all the land below the high terrace is delimited with a polygon.

Next, the distance from that polygon can be calculated using

Toolbox > Spatial Analyst Tools > Distance > Euclidean Distance...

for a more complex approach consider using a "cost distance" model such as Tobler's hiking function based on travel time that can be implemented in

Toolbox > Spatial Analyst Tools > Distance > Cost Distance...

The resulting distance GRID can be classified into two regions: one within (with 0 values) and one outside of (1 values) the specified travel distance (or time) using Spatial Analyst > Reclassify...

Next, the land under 15 degree slope can be selected by reclassifying the output from a Spatial Analyst Slope calculation. Again if two GRIDs are specified with 0 and 1 values.

Finally, these output GRIDs can be combined in raster calculator (GRID1 + GRID2) and all the places with "2" in the output are in the overlap zone between the two GRID files.

 The output might be converted to Vector (polygon) and mobile GIS can be used to guide the survey to remain within the bounds specified with the model.

Consider do a swath of "100%" coverage in order to test the assumptions of your model. What kinds of sites were found with the 100% survey that were missed in the model survey?

Keep in mind that you are not modeling human behavior -- you are modeling the areas with high probability of encountering sites in modern contexts.

---

Rule based model using ModelBuilder in ArcGIS

This week we will make use of a lab developed by UCSB Geography that uses a simple Rule-based predictive model based on Anabel Ford's research on the border of Belize and Guatelamala. We will take the results of this model and evaluate it in JMP.

Begin by going to the UC Santa Barbara Geography 176b lab 4 page.

Go through Exercise II of Lab 4 "Developing a Predictive Model".
Note: choose a larger sample. We want at least 100 sites in the output.

At the end of the Geography lab when you have arrived at the point with a file entitled Arch_Sites_ID_Freq return to this page

Now export this data to a comma-delimited text file.

• Right click the Arch_Sites_ID_Freq table and choose Data > Export…
  Click the Folder and save it locally, but change the file type to TXT

Analysis in JMP

• Now open the program JMP 5.1 from the Statistics folder on your desktop.
• Open the data table
• Chi-Squared and other analyses functions are found under

Analyze > Fit Y by X (Use the SITE field for Y)

• Logistic Regression is found under

Under Analyze > Fit Model

• Click SITE and Click the Y button
• Select the other variables (except ObjectID and Frequency) and click the Construct Model Effects: Add button

• Click Run Model

See the discussion on this webpage for interpreting the results
We will further discuss analysis in class.

Week 9 - Anisotropic cost surfaces and Least-cost paths

Week 9 - Anisotropic Cost surfaces

Introduction: Non-Cartesian Distance Units
Spatial analysis in anthropology is frequently based on Cartesian coordinates that describe space in terms of regular units on a grid coordinate system. The UTM system is a good example of a Cartesian coordinate system in metric units. GIS permits the calculation of distance costs in terms of non Cartesian units that, some have argued, are a better reflection of real perspectives and human (agent) decision-making.

Consider your commute to the University today. You may calculate it in terms of linear distance units like miles or kilometers, but you likely arrived here by any number of ways: bike, bus, walking, or private car. Furthermore, there are added complexities to some modes of travel, such as catching the proper bus or finding parking for your car.

In terms of time budgeting, you might be better off considering the commute to the university in terms of time units (hours) rather than linear distance units. In terms of a general model we could assign some costs to certain features: wading across the river perhaps takes 5x longer per meter than crossing land. Bushwacking through chaparral takes 10x longer. These types of costs can be implemented systematically in the GIS in order to convert distance measures in Cartesian space (e.g., UTM) into time. More explicit ecological approaches might convert costs into calories.
Clearly these kinds of cost-surfaces will involve many assumptions about transportation and impedance.

In this week's exercise we will perform a cost distance calculation using a customized cost function that reflects empirical data published by Tobler, 1993. Tobler's function estimates time (hours) to cross a raster cell based on slope (degrees) as calculated on a DEM.

I have converted data provided by Tobler into a structure that ArcGIS will accept as a "Vertical Factor Table" for the Path Distance function. In other words, ArcGIS makes these sorts of calculations easy by allowing you to enter customized factors to the cost function.

First, skim over the ArcGIS 9 description of the PathDistance function.

PathDistance is an elaboration of Cost Distance algoritm, as discussed in class.

---

PART A. ISOTROPIC TIME ESTIMATION

1. Distance and time estimates based on 4 km/hr speed on an isotropic surface

This exercise begins by calculating distance and estimating time the old fashioned way, as you would do on a map with a ruler.

We will begin by creating an isotropic cost surface and then generating 15 min isolines on this surface.

• From the Callalli.zip file load "All_ArchID", "Callalli_DEM", and "hydro_lines100k" into Arcmap

• Open the attribute table for All_ArchID and choose the rows with ArchID = 675 and ArchID = 985.

Hint: Sort Ascending ArchID column, and hold down ctrl button while you click the left-most column in the table for those two rows.

• Go to Toolbox > Spatial Analyst Tools > Distance > Euclidean Distance

Input Feature: All_ArchID
Output Dist Raster: Iso_dist1
<click folder and save it in the same DEM folder>
Leave the other fields blank.

• Before clicking OK click the Environments… button at the bottom of the window.

• Click the General Settings… tab and look at the different settings. Change the Output Extent field to read "Same as layer callalli_dem".

2. Create raster showing isotropic distance in minutes

The output is a raster showing the metric distance from the two sites.
Let's assume for the purposes of this example that hiking speed is 4 km/hr regardless of the terrain, which works out to 1000m each 15 min.

• To transform the isodist1 grid into units of time (minutes) we can perform a Spatial Analyst > Raster Calculator expression using this information:
  15 min / 1000 meters = 1 min / 66.66 meters
  

How would you construct that equation in Raster Calculator to get the raster to display in units of minutes?
If you've done it right the output raster (Calculation) will range in value from
0 to 112.614
Hint: divide the raster by 66.66

• When you have this raster right click and choose "Make Permanent…", and call it "isodist_min". Remove the Calculation grid and add this "isodist_min" grid to your project.

3. Convert to isochrones

• Create contours using the output raster with
  Spatial Analyst > Surface Analysis > Contour…

• Then use the good Calculation raster as your input surface, choose 15 as your interval and use the defaults for the rest. Save the file out as "isochrone15".

What do you think of the results of these lines?

This photo was taken facing south towards Taukamayo which lies in the background on the right side of the creek in the center-left of the photo. Taukamayo is the western-most of the two sites you just worked with in Arcmap. You can see how steep the hills are behind the site and on the left side of the photo you can see the town of Callalli for scale. Clearly the land is very steep around the site, especially in those cliff bands on the south end of the DEM. There are also cliffbands on the north side of the river but the river terrace in the foreground where the archaeologists are standing is quite flat.

---

PART B. ANISOTROPIC COST SURFACE

We will use ArcWorkstation GRID program for this calculation because the custom (directionally dependent) slope calculation is not supported directly in the Arcmap CostDistance or Pathdistance functions.
ArcGRID dates to before the Shapefile and Geodatabase formats were used, so we must work with GRID rasters in this program.

Step 1: Create the source_grid

• Once again, open the attribute table for All_ArchID and choose the rows with ArchID = 675 and ArchID = 985.
• Set the extent of the output grid
  Spatial Analyst > Options > Extent tab > Analysis extent: Same as layer "callalli_dem"

Convert the two points to a GRID layer

• Spatial Analyst > Convert… > Features to Raster…

Input: All_ArchID
Field: ARCHID
Output (default)
Output raster: click folder and save into /DEM/ folder. Call it "sites"

Note: For today's exercise you can not have spaces anywhere in the path to these files.

Turn off the other layers and look closely at the two sites in the raster you just created. Do you see a square at each site?

Step 2: Calculate PathDistance in ArcWorkstation GRID

• Start ArcGRID
• Start Menu > Programs > ArcGIS > ArcInfo Workstation > GRID
• Click on the GRID window with the prompt that reads "Grid: " to make it active.
• Type "Help" (leave out the quotes)
• Then in the Help window click the Index tab and type "Pathdistance"

You will see a description of the function with a breakdown of how it is issued. It looks like this with a variety of required and optional arguments.

PATHDISTANCE(<source_grid>, {cost_grid}, {surface_grid}, {horiz_factor_grid}, {horiz_factor_parm}, {vert_factor_grid}, {vert_factor_parm}, {o_backlink_grid}, {o_allocate_grid}, {max_distance}, {value_grid})

• Scroll down through this page. As you can see, it is a comprehensive description, and it has a lot of similarities to the help description webpage we saw earlier. Close the Help box.
  

The formula used by PATHDISTANCE to calculate the total cost from cell a to cell b is:
Cost_distance = Surface_distance * Vertical_factor * (Friction(a) * Horizontal_factor(a) + Friction(b) * Horizontal_factor(b)) /2)

In ArcInfo GRID the PATHDISTANCE function can be used to conduct anisotropic distance calculations if we supply the function with a customized Vertical Factor table with the degree slope in Column 1 and the appropriate vertical factor in Column 2. The vertical factor acts as a multiplier where multiplying by a Vertical Factor of 1 has no effect. The vertical factor table we will use was generated in Excel and it reflects Tobler's Hiking Function by using the reciprocal of Tobler's function. This function was used in Excel:

TIME (HOURS) TO CROSS 1 METER or the reciprocal of Meters per Hour =0.000166666*(EXP(3.5*(ABS(TAN(RADIANS(slope_deg))+0.05))))

Thus for 0 deg slope which Tobler's function computes to 5.037km/hr, the result should be 1/5037.8 = 0.000198541

You can download the file that we will use for these values here.

Right-click ToblerAway.txt, choose"Save Link as..." and save it in the same folder as your GRID files (the reciprocal ToblerTowards.txt is used for travel in the opposite dirction, towards the source).

An abbreviated version of this ToblerAway file looks like this

 

Slope (deg)	Vertical Factor
-90	-1
-80	-1
-70	2.099409721
-50	0.009064613
-30	0.001055449
-10	0.00025934
-5	0.000190035
-4	0.000178706
-3	0.000168077
-2	0.000175699
-1	0.000186775
0	0.000198541
5	0.000269672
10	0.000368021
30	0.001497754
50	0.012863298
70	2.979204206
80	-1
90	-1

 

• In Windows browse to the folder that holds the Callalli_DEM, Site GRIDs, and the ToblerAway file.
• Look at the PATH to this directory (confirm that there are no spaces and only alphanumeric characters)

• Set the Working directory in GRID

• At the GRID: prompt type
• &wo <complete path to DEM>

on my computer this command reads: &wo c:\gis_data\anth197\dem\

• If it is successful, then type "lg" at the prompt.
  You should see a list of the grid contents of the working directory.
  

• Issue this command at the GRID: prompt
  Pathdistance
• You'll see an example of how to strcuture this command
• Following that example, type the following at the GRID: prompt
  aniso_hours = Pathdistance (source_grid , # ,DEM_grid, #, #, DEM_grid, "TABLE ToblerAway.txt", aniso_bklk)
  

Substituting "sites" for source_grid and "callalli_dem" for DEM_grid in the above function. Make sure you type it exactly! If you have an error, use the up arrow key to re-type the previous command and the left/right arrow keys to move around. Include the # sign. # tells GRID to use the default values.

• When the function runs successfully (i.e., no error), return to Arcmap.

• Add the resulting grid to Arcmap (aniso_hours). Does the file range from 0 to 2.5?

Why aren't the values larger? Recall what units the Tobler_Away function calculates?

We need to multiply this result by 60 because…. It's in hours.

• Spatial Analyst > Raster Calculator…
  [aniso_hours] * 60
• Right-click the Output Calculation and Make Permanent… Call it "aniso_min"

• Now generate 15 min contours on this layer as you did earlier and call the output "aniso15".
• Turn off all layers except Callalli_DEM", "Hydro", "isochrone15" and "aniso15".
• Do you see the difference in the two cost surfaces?
  

Using the Info tool (the blue 'i') you can point-sample distances along the way.

The differences between the two surfaces are interesting

• Spatial Analyst > Raster Calculator...
• [aniso_min] - [isodist_min]

Look at the result. What are the high and low values showing?

---

PART C. GENERATING LEAST-COST PATHS BETWEEN SITES

Recall that you generated a Backlink grid called Aniso_bklk as part of your ArcGRID work. We will now use that to calculate least-cost paths between the two sites and other sites in the region.

• Add Backlink Grid to Arcmap called "aniso_bklk".

Look at the results. Recall how Backlink Grids work (read the Help on COST SURFACES), do the values 0 through 8 make sense?

Choose four sites from ArchID for this calculation
588, 611, 811, 835

• How would you construct this selection in ArchID from the Attribute Table using Options > Select by Attributes…?

It should look something like this
[ARCHID] = 588 OR [ARCHID] =611 OR [ARCHID] = 811 OR [ARCHID] = 835

• Now close the attribute table. You have four sites selected around the perimeter of the study area?

• Choose Toolbox > Spatial Analyst Tools > Distance > Cost Path…

Input Feature: All_ArchID
Destination Field: ArchID
Input Cost Distance Raster: aniso_hours (use the hours not the minutes one)
Input Cost Backlink Raster: aniso_bklk

Note that the output is a raster GRID file. Wouldn't these be more useful as Polylines?

• Use Spatial Analyst > Convert > Raster to feature….

Input Raster: <the name of your cost paths file>
Field: Value
Geometry type: Polyline

Zoom in and explore the results with only the following layers visible:

Callalli_DEM, Hydro_lines100k, aniso_minutes isolines, and the cost-paths you just generated. Note how the paths avoid steep hills and choose to follow valleys, as you might do if you were planning to walk that distance.

The Lab 4 assignment (due next week at the beginning of class) involves conducting these analyses on your own dataset.

To quit GRID type "quit" at the prompt.

Week 10 - Viewshed and Cumulative Viewshed Analysis

Week 10 In Class Exercise

VIEWSHED ANALYSIS

There are several types of viewshed analysis available in ArcGIS.
We will visit two of these types using the Callalli study area.

Instead of using the data from before, I've prepared new files because we need a larger DEM and a Sites shapefile with time periods assigned.

Download the View.Zip file and uncompress to a path with no spaces.

As with other data used in this class, this Sites dataset is based on my dissertation data set, but the attributes are not the actual data so don't compare this Sites file with what is in my dissertation.
 

I. Setup the project in Arcmap.

• Add the Sites shapefile.
• Add the 30m ASTER DEM from \dem_large\COLCA_ASTER
• Add the hydro layer from the Callalli geodatabase known as "Hydro_lines100k" if you have it.

Look at the coordinates. Is this in UTM or in Decimal Degrees? With Viewshed analysis linear units (like Meters) are necessary to accurately calculate distances.

Look at the Attribute table for Sites. You're familiar with most of these attributes from previous labs.

We'll use the "Period" field to differentiate sites from different time periods in this study.

The values are

Formative (2000BC - AD400)
MH Middle Horizon (AD400-AD1100), there are no MH sites in this dataset
LIP Late Intermediate Period: (AD1100-AD1476)
LH Late Horizon (AD1476-AD1532)

 

2. How do we control the viewshed calculation?

Please see the explanation on this webpage: ArcGIS Help - Viewshed

The optional viewshed parameters are SPOT, OFFSETA, OFFSETB, AZIMUTH1, AZIMUTH2, VERT1, and VERT2<. These will be used if they are present in the feature observer attribute table.

The only two attribute variables we are concerned with at this point are OFFSETA (height of viewer) and RADIUS2 (the maximum radius of the viewshed calculation).
The viewer's eyes are at 1.5m above the ground, and we want to know the visible area within 5 km of each site.

• Make sure nothing is selected.
• Open the Attribute Table for the Sites layer
• Choose Options > Add Field…
• Call it OFFSETA, make the type FLOAT and the Precision 2 and the scale 1.

Precision sets the number of significant digits, while the Scale is the location of the decimal point from the right side of the value. This allows the field to store 1.5.

• Use Calculate Values... command to put 1.5 in the field for the whole table.

• Choose Add field... again
• Call it RADIUS2 and leave it as the default, short integer

Since we want to limit the value of the view to 5 km, what should the value be in that goes in this field? What are the spatial units of this map?
You can use Calculate Values... command to fill the RADIUS2 field with the value 5000 all the way down.
 

II. Quick Viewshed analysis

• go to Spatial Analyst toolbar > Surface Analysis > Viewshed…

Input: Colca_Aster
Observer Points: Sites
Use the defaults and allow the output to go into Temporary.

Look at the result. What is this showing? Is this informative?

• Put the Colca_HS (hillshade) layer above the Viewshed output at 60% transparency.

This help you to visualize what is happening.
 

What are some problems with this output?
If we use this quantitatively do you see any potential issues with edge effects?

To quickly resolve problems in this dataset we have to subset the data:

• Zoom out so you can see the project (click the globe)
• Right-click the Sites layer in the table of contents,
• Choose Select > Select All
• Choose the selection arrow (white arrow on blue shape) and draw a selection box around all sites EXCEPT the two sites in the top-left part of the study area.

• Right-click the layer again and choose Export Data… and save out the shapefile and call it "Sites_sub". Add the new layer and remove the old one.

Can you think of another way to solve the Edge effects problem? Two simple solutions: (1) throw out samples close to the edges, (2) try to acquire a larger DEM in the first place.

III. Viewshed analysis - differences between time periods

What is missing from the previous analysis was a theoretical question guiding the inquiry. Obviously, you can select a single site and run a viewshed and find out the resulting area. But how is this different from just going to the site and looking around and taking photos?
You could also select a line and find the viewshed along a road, for example. However, computers can answer interesting questions by looking at general patterns with larger datasets. This is where computers give you an advantage because you're repeating many small operations.

We want to answer questions such as:

How do viewsheds change based on the type of site that is being evaluated?
Are Late Intermediate sites more or less likely to be constructed such that they can view one another?

We can calculate separate viewsheds for each group of sites in our table by manually selecting each group from the Attribute Table and running the viewshed calc.
This is a good application for ModelBuilder, except that Batch processing is not available in ModelBuilder until version ArcGIS 9.2 and we are still using ArcGIS 9.1 in the lab.
 

1. Calculate viewshed for each major group:

• Open the Sites_sub Attribute table, Sort Ascending on the "Period" field.
• Select only the Formative sites
• Use Spatial Analyst > Surface Analysis > Viewshed…
• Save the result as "Form5km" in the view folder
• MAKE SURE the INPUT SURFACE IS COLCA_ASTER.
• Repeat the above process two more times with LH and LIP, calling the output GRID files LH5km and LIP5km respectively.

2. View the results

Have a look at the output GRID Attribute table. The VALUE field indicates how many of the sites can view a given cell, and the COUNT field indicates how many cells fall into that category.

In other words, in Form5km GRID the VALUE = 3 row shows that 1716 cells are visible from 3 sites but no one cell is visible from all four Formative sites in this group.

We could calculate the number of cells in view per site, or other types of averages.
For example, in the Sites Attribute table there is a SiteType field that indicates that some of the LIP sites are Pukaras. These are hilltop fortresses that have notoriously good views. However… there's a problem. The problem lies in the bias sample we have because sites tend to aggregate around resource patches or other features.
In these areas our dataset has high "intervisibility" because it reflects aggregation within the 5km buffer.
In other words, many sites can see a particular cell in those situations where there are many sites in a small area!

We can get around this problem by calculating viewshed for random site locations as representative of "typical" views in the area. We will then compare our site views against this typical viewshed.

IV. Cumulative Viewshed Analysis

Another way to calculate viewsheds is more powerful yet because it allows you to compare the result against a "typical" viewshed for the area.

In version 9.1 of ArcGIS we still need to use the command line GRID program to accomplish this task. Thus we have to convert out files to coverage or GRID to view them in the older GRID program.

I created a Shapefile with 500 random points was created in Hawth's Tools (available from Arcscripts and SpatialEcology.org, as you learned previously in this class) and there is a minimum of 50m spacing between each point.

Download Random.zip and unzip into the same folder as the Colca DEM folder.

Look at the Attribute table and note that the OffsetA and Radius2 fields were added, as above.

We must convert the Rand500 point file to Coverage in order to use it with GRID.
Choose
Toolbox > Conversion > To Coverage > Feature Class to Coverage….

Save the coverage as "rand500_cov" into the /view/dem_colca/ folder.
That way everything is in one folder.
 

• Type
  &wo and the complete path to your /view/dem_colca/ folder
• Issue the following command
  Randvisib = visibility ( colca_aster , rand500_cov, point , frequency )

When it completes return to Arcmap and add the resulting RandVisib grid.

Type 'q' to quit GRID.

Now use the Spatial Analyst > Zonal Analysis ...
Tool to answer the question: Sites from which of the three time periods have the highest mean visibility with respect to the RandVisib grid?